(i) Wavelet-based structural and random noise modelling

One substantive argument favoring the use of wavelet methods specifically in analysis of brain imaging data that is based on the expectation that the brain may often demonstrate broadly fractal properties. The word fractal was originally coined by Mandelbrot (1977) to define a class of objects with the characteristic property of self-similarity (or self-affinity), meaning that the statistics describing the structure in time or space of a fractal process remain the same as the process is measured over a range of different scales. In other words, the structure of the process is approximately scale invariant or scale free. Many ways in which wavelets are technically attractive for statistical analysis of fractal processes are as follows: wavelet-based methods effect a multiresolution decomposition that is advantageous for analysis of scale-invariant processes; (ii) wavelet-based methods are theoretically optimal whitening and provide KL expansions for long-memory (1/f-like) processes and many issues in estimation and hypothesis testing are simplified by independence; and wavelets can be used to construct good estimators for th noise process parameters. Our contributions were on these aspects in fMRI data analysis.

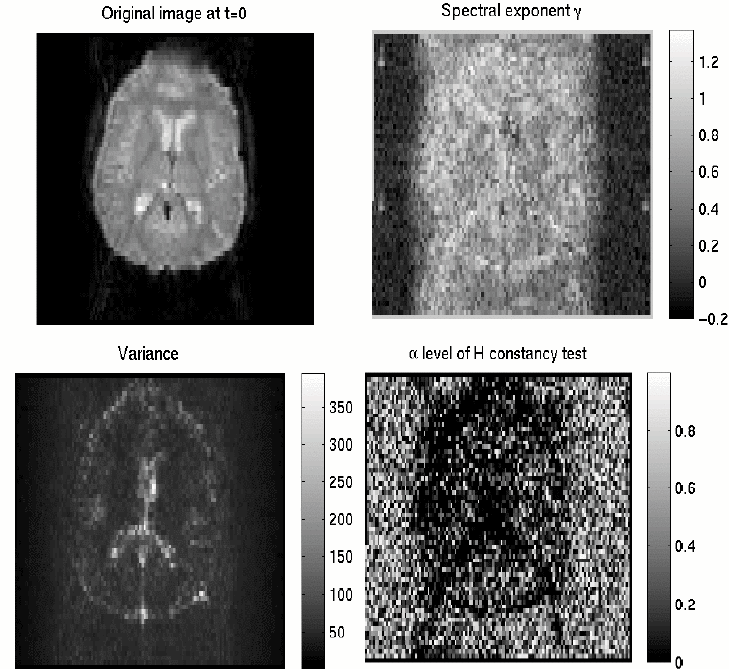
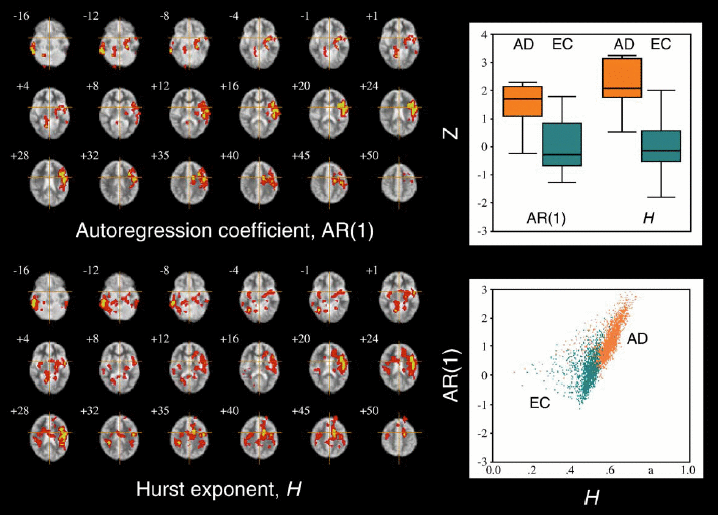
1/f-like characteristics of fMRI time series. It is clear that both time series have disproportionate power at low frequencies confirmed by the PSD plot.	Spectral exponents of fMRI data acquired under no-task conditions.	fMRI data can even exhibit locally stationary 1/f behavior especially in the cortex.	Note that voxels with large Hurst exponents (or AR(1) coefficients) tend to be concentrated symmetrically in cortical regions, whereas voxels with small negative values tend to be concentrated around ventricles and are associated with high variance. The swarm of (pink) points corresponding to estimates of H and AR(1) in voxels located outside the brain, which show that the background instrumental noise in fMRI is approximately white.
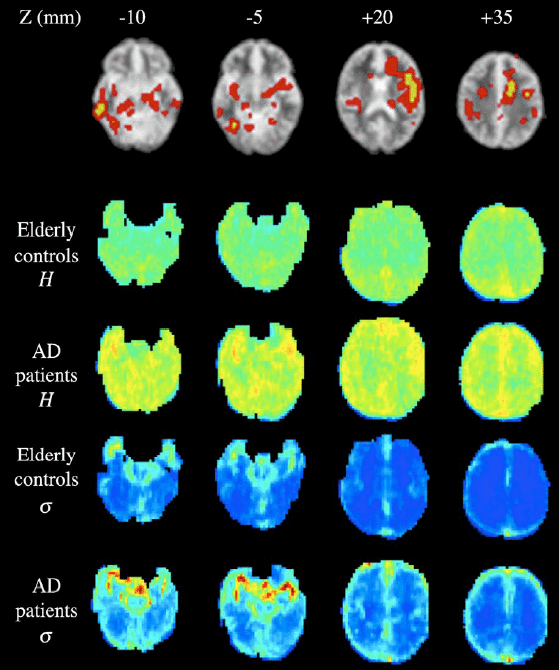
	Effects of Alzheimer’s disease (AD) on Hurst exponent estimated by wavelet-ML in resting state fMRI data.	Whole brain maps showing location of significant differences between patients with Alzheimer’s disease (AD) and an elderly control group of agematched volunteers (EC) in terms of the Hurst exponent H and the first-order autoregression coefficient AR(1). Note the superior sensitivity of the Hurst exponent in detecting AD-related anatomical changes.

(ii) Wavestrapping of 1-D time series, 2- to 3-D spatial maps and 4-D spatiotemporal processes

Data resampling by permutation or bootstrap offers many advantages for inference on functional neuroimaging data—in particular, it obviates the need to make unrealistic assumptions about spatial auto-covariance and other distributional aspects of the data. Perhaps for these reasons, an appropriate nonparametric test can have superior sensitivity compared to a parametric alternative. Moreover, there are many statistics of potential interest in brain mapping, for example, spatial and multivariate statistics, that do not have theoretically tractable or well-established distributions under the null hypothesis and therefore cannot properly be tested parametrically. In contrast, almost any statistic of interest may be accessible to inference on the basis of an appropriate resampling scheme (for examples, respectively, of resampling spatial and multivariate statistics in brain mapping. However, designing an appropriate resampling scheme for statistics estimated by analysis of a functional MRI time series is complicated by nonindependence of the observations under the null hypothesis. Owinf ot its decorrelating (and even stationarising) properties for a wide class of processes, orthogonal wavelet-based transforms provide an alternative device for the strategy of resampling. We have demonstrated the theoretical and practical advanatges of wavestrapping in a series of publications, for a variety of processes including 1/f and seasonal processes.

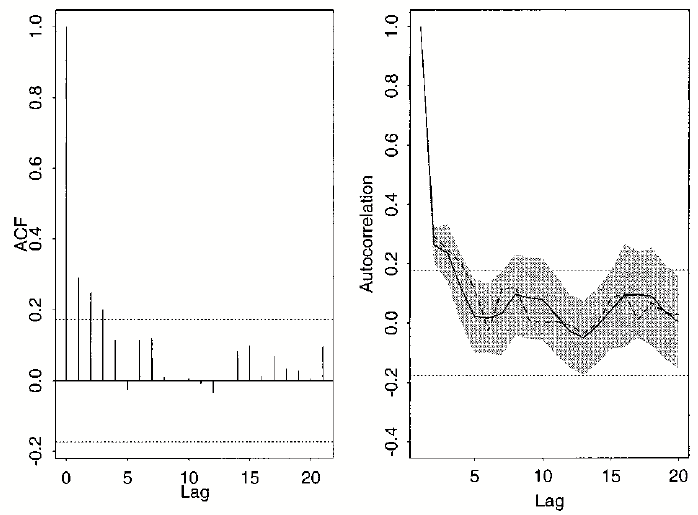
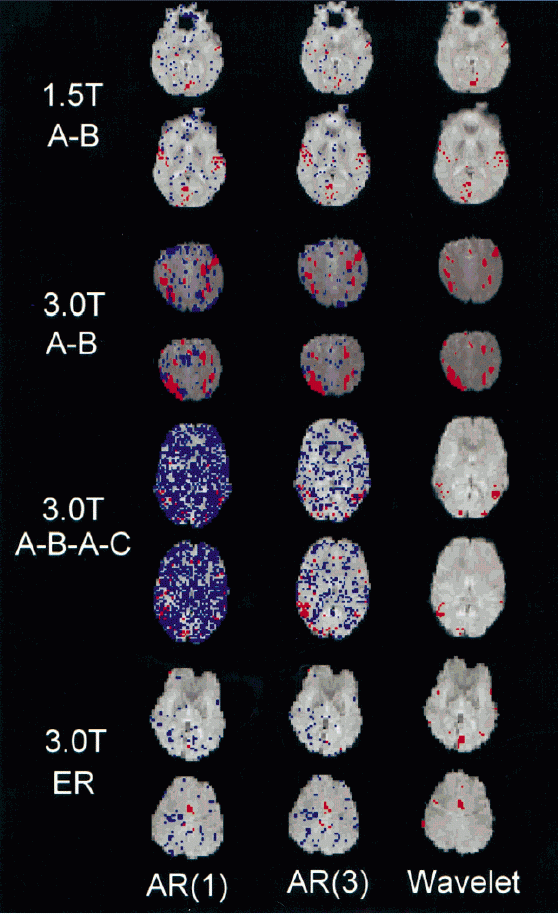
Wavelet resampling in the original (spatial, temporal) domain preserves the ACF and the PSD  of the stationary original data.		Brain activation mapping of experimental fMRI data based on different treatments of residual autocorrelation. Wavelet resampling is considerably more robust than the AR prewhitening schemes in dealing with some of the higher field datasets, but of approximately equivalent sensitivity.

(iii) Wavelet-based estimators for parametric and semiparametric models

We have specified the fMRI regression problem with long-memory noise and possibly with a structural non-parametric component directly in the wavelet domain. As noted earlier, the orthonormal DWT is approximately a Karhunen–Loève expansion, which allows to whiten the noise. Simuiltaneously, the sparsity of the wavelet transform ensures a parcimonious representation of the nonparametric unknown part. Efficient algorithms for estimating both the noise and the signal (parametric and non-parametric parts) were proposed and theoretically studied.

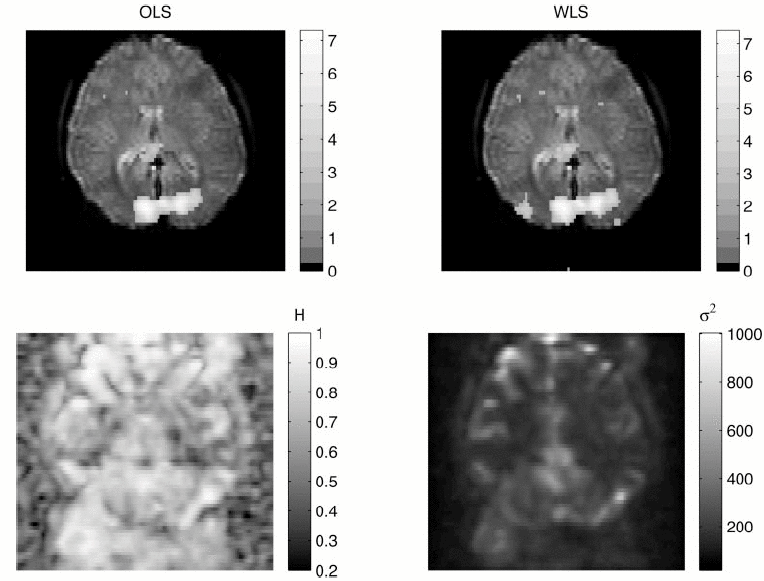
Type I error calibration curves. Note the superiority of the wavelet-domain LS approach.	Signal and noise parameters maps for a visual task.	Semiparametric models (coming soon).

(iv) Wavelet-domain hypothesis testing for estimation of spatially extended statistic map

We proposed a framework combining wavelet-based methods and statistical hypothesis testing for activation mapping of human fMRI data. In this approach, we emphasise convergence between methods of wavelet thresholding or shrinkage and the problem of hypothesis testing in both classical and Bayesian contexts. Specifically, our interest was focused on the trade-off between type I probability error control and power dissipation. We presented a technique for controlling the false discovery rate at an arbitrary level of error in testing multiple wavelet coefficients generated by a 2D discrete wavelet transform (DWT) of spatial maps of fMRI time series statistics. We also described and applied change-point detection with recursive hypothesis testing methods that can be used to define a threshold unique to each level and orientation of the 2D-DWT, and Bayesian methods, incorporating a formal model for the anticipated sparseness of wavelet coefficients representing the signal or true image. The sensitivity and type I error control of these algorithms were comparatively evaluated by analysis of null images and an experimental data set acquired from normal volunteers during an event-related finger movement task. We showed that all three wavelet-based algorithms have good type I error control (the FDR method being most conservative) and generate plausible brain activation maps (the Bayesian method being most powerful). We also generalised the formal connection between wavelet-based methods for simultaneous multiresolution denoising/hypothesis testing and methods based on monoresolution Gaussian smoothing followed by statistical testing of brain activation maps.

Click on each link to download the corresponding movie (activation volume rendering).

FDR-based map.	Recursive testing map.	Bayesian testing map.	SPMM FWHM=6mm	SPM FWHM=10mm
All maps were thresholded at a significance level of 0.01 (height-corrected for SPM). Note that significance of the ipsilateral cerebellar signal is conditional on kernel size and that plausible signals in medial premotor cortex and ipsilateral somatosensorimotor cortex recovered by multiresolution analysis/ multiple hypothesis testing in the wavelet domain are not evident in these results of monoresolution smoothing followed by multiple hypothesis testing in the spatial domain.